4. How can I solve a binomial distribution on a TI-84 calculator?

On a TI-84 calculator, you can use:

• binompdf(n, p, x) → Finds the probability of exactly x successes.
• binomcdf(n, p, x) → Finds the cumulative probability of x or fewer successes.

You can access these by pressing:
2nd → VARS → scroll to A:binompdf( or B:binomcdf(

5. What does the graph of a binomial distribution look like?

A binomial distribution graph is a bar graph that shows the probability of each possible number of successes.

• If p = 0.5, the graph is symmetric.
• If p < 0.5 or p > 0.5, the graph is skewed.
• The bars represent the probability for each k (number of successes).

6. How is the binomial distribution different from the normal distribution?

• The binomial distribution is discrete (counts whole number successes).
• The normal distribution is continuous, so it can take any value within a given range.
• The binomial distribution has two outcomes per trial; normal distribution describes outcomes that spread out smoothly across a range.
• When n is large and p is not too close to 0 or 1, the binomial distribution can be approximated by a normal distribution.

7. How do I find the mean of a binomial distribution?

The average (mean) number of successes in a binomial distribution is calculated using:

μ=n×p

where:
n = total number of trials
p = probability of success in each trial

8. What is the formula for the standard deviation of a binomial distribution?

The standard deviation ($\sigma$) of a binomial distribution is:

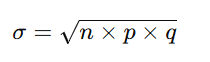
Where:

• n = number of trials
• p = probability of success
• q = 1 – p (probability of failure)

9. Is the binomial distribution discrete or continuous?

The binomial distribution is discrete because it counts whole numbers of successes (0, 1, 2, …, n).

10. What are some real-life uses of the binomial distribution?

Examples include:

• Predicting the number of heads in coin flips
• Counting defective products in manufacturing
• Survey responses (yes/no)
• Successes in games or sports (like free throws made)

Conclusion

The Binomial Distribution Calculator makes it easy to compute the probability of a certain number of successes across multiple independent trials. Whether you are a student, teacher, or researcher, this tool helps save time and ensures accuracy in solving binomial distribution problems. Use it to explore probabilities, check your work, or enhance your understanding of binomial concepts.

Disclaimer

This Binomial Distribution Calculator is designed for educational and informational use only. While we aim to provide accurate results, we do not guarantee error-free calculations. Please verify important results manually or with other trusted methods, especially for academic, professional, or official use. We are not responsible for any decisions or actions taken based on the use of this calculator.