Welcome To Our Negative Binomial Distribution Calculator
Use this Negative Binomial Distribution Calculator to find probabilities in repeated trials until r successes. Includes formula, steps, and examples.
Negative Binomial Distribution Calculator
Table of Contents
Related Calculator:

Negative Binomial Distribution Calculator – With Steps & Cumulative Probability
Introduction
The negative binomial distribution is a powerful statistical model used to calculate the probability of a specific number of failures before a fixed number of successes occurs in a series of independent Bernoulli trials. When paired with a calculator, it becomes even easier to compute probabilities for complex scenarios.
What is the Negative Binomial Distribution?
The negative binomial distribution models the number of failures (x) before a specified number of successes (r) occurs in a sequence of independent trials. It is different from the binomial distribution, which deals with the number of successes in a fixed number of trials.
Key Parameters:
- x = number of failures
- r = number of required successes
- p = probability of success on a single trial
- q = 1 – p = probability of failure
Negative Binomial Probability Formula

What is a Negative Binomial Distribution Calculator?
A negative binomial distribution calculator automates the above formula. You input values for:
- Number of required successes r
- Probability of success p
- Number of failures x
And the calculator gives you:
- Probability for exact value of x
- Optionally, the cumulative probability up to a value
This saves time and reduces errors in manual calculations.
Why Use a Calculator?
Using a negative binomial distribution calculator with steps is helpful because:
- It eliminates human error
- Provides step-by-step breakdowns
- Calculates both individual and cumulative probabilities
- Great for students, teachers, and professionals dealing with statistical data
Use Cases of Negative Binomial Distribution
| Field | Application |
|---|---|
| Healthcare | Modeling time until a disease is cured after several treatments |
| Quality Control | Estimating number of defective items before reaching a target of functioning units |
| Sports | Predicting failures (missed shots) before a player scores a fixed number of goals |
| Marketing | Calculating number of failed calls before reaching a set number of successful leads |
How to Use the Negative Binomial Distribution Calculator
Here’s how to use the calculator step-by-step:
Inputs:
- r: Number of required successes
- p: Probability of success
- x: Number of failures before success
Output:
- P(X = x): Probability of getting exactly x failures
- Optionally: P(X ≤ x): Cumulative probability
Example 1: Exact Probability
Problem:
A basketball player has a 40% chance of making a free throw. What is the probability that he will miss 3 times before making 2 successful throws?
Given:
- r = 2
- p = 0.4
- x = 3
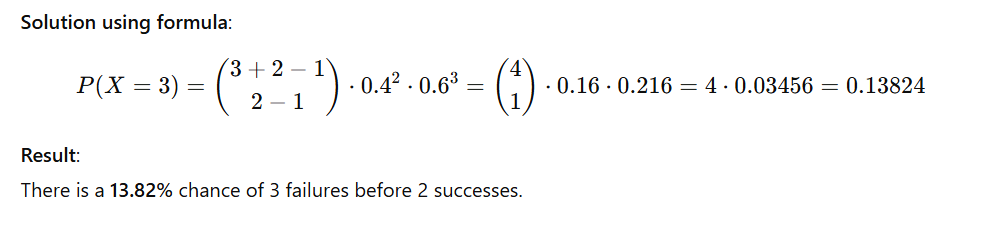
Example 2: Cumulative Probability
Problem:
Using the same player and conditions, what is the probability of having 3 or fewer failures before 2 successful throws?
Approach:
Use the cumulative negative binomial distribution calculator.
![]()
Sum the probabilities from x = 0 to x = 3 using the calculator.
Result:
The cumulative probability is approximately 76.4%
Comparison: Binomial vs Negative Binomial
| Feature | Binomial Distribution | Negative Binomial Distribution |
|---|---|---|
| Fixed number of trials | Yes | No |
| Fixed number of successes | No | Yes |
| Random variable | Successes | Failures |
| Use case | Predict how many successes in fixed trials | Predict failures before hitting success target |
FAQ – Negative Binomial Distribution Calculator
Q1. What is the difference between binomial and negative binomial distributions?
The binomial distribution calculates the probability of a fixed number of successes in a set number of trials. In contrast, the negative binomial distribution calculates the probability of a fixed number of failures occurring before a certain number of successes is achieved.
Q2. Can this calculator compute cumulative probabilities?
Yes. A cumulative negative binomial distribution calculator can compute probabilities such as P(X≤x), which tells you the chance of experiencing up to x failures before reaching the required number of successes.
Q3. Can I use decimal values for the success probability?
Absolutely. The probability of success p can be any decimal value between 0 and 1, such as 0.25, 0.5, or 0.85. The calculator supports decimal input to reflect real-world scenarios more accurately.
Q4. Is this calculator suitable for academic or classroom use?
Yes. This calculator uses the standard mathematical definition of the negative binomial distribution and is widely used by students, researchers, and educators for statistical analysis.
Q5. What happens if I input an invalid value?
If you enter values outside the valid range (e.g., negative numbers or a probability greater than 1), the calculator will either show an error or return a result of 0 probability. Always double-check your input values.
Conclusion
The Negative Binomial Distribution Calculator simplifies complex probability computations by providing fast and accurate results. Whether you’re calculating the probability of failures before a success threshold or analyzing cumulative distributions, this tool saves time and avoids manual errors.
It is ideal for academic, research, and professional applications where understanding statistical patterns is essential. By using this calculator, you gain clarity and confidence in analyzing real-world events that follow negative binomial behavior.
Disclaimer
This tool is intended for educational and informational purposes only. While the underlying formulas follow standard statistical theory, it should not be used as the sole decision-making resource for business-critical or professional analyses. Users should verify results with additional methods or consult a statistician for advanced or high-stakes applications. The creators of this tool are not liable for decisions made based on its output.