Use our Binomial CDF Calculator to find cumulative probabilities easily. Perfect for AP Statistics, SAT, ACT, and college-level stats problems.
Binomial CDF Calculator
Binomial CDF Calculator
In high school and college-level statistics courses across the USA—like AP Statistics, Precalculus, and Intro to Stats—you’ll often encounter binomial distribution problems. One of the most common tasks is calculating the cumulative probability: the chance of getting x or fewer successes in n trials.
What Is Binomial CDF?
The Binomial Cumulative Distribution Function (CDF) calculates the probability that a binomial random variable 𝑋 is less than or equal to a given value 𝑥.

In simpler terms:
It tells you the probability of getting x or fewer successes in n trials.
Why Binomial CDF Matters in U.S. Schools
Binomial CDF is part of:
- AP Statistics curriculum (College Board)
- SAT / ACT Math sections
- College Statistics (MATH 101, PSYCH 210, etc.)
Used in:
- Multiple-choice test simulations
- Drug efficacy trials
- Sports shot success analysis
- Quality control in economics
Binomial CDF Formula
The formula for binomial CDF is:

How to Use Online Binomial CDF Calculator
Visit a trusted calculator (e.g. binomialdistributioncalculator.com).
Enter:
𝑛 : number of trials
𝑝 : probability of success
𝑥 : number of successes
Select the type of cumulative probability:
P(X ≤ x)
P(X ≥ x)
P(a < X ≤ b)
Click “Calculate” to get your result.
Benefits:
- Fast and accurate
- No login or installation needed
- Good for homework and last-minute SAT/AP practice
How to Use Binomial CDF on TI-84 / TI-83
Steps:
- Press 2nd then VARS to open the DISTR menu.
- Scroll to and select binomcdf(.
Enter:
- Binomcdf (n,p,x)
Example:
- Binomcdf (10,0.25,4)
Press ENTER.
- This gives you P(X ≤ 4) for 10 trials with success probability 0.25.
Real SAT / AP Stats Binomial CDF Example
Question:
A student guesses on all 10 multiple-choice questions of a test. Each question has 4 choices. What’s the probability of getting 4 or fewer correct?

Upper and Lower Bound Interpretation
TI calculators don’t allow lower and upper bounds directly, but you can calculate ranges by subtraction.

Binompdf vs Binomcdf on TI Calculators
| Function | Meaning | Formula | Use Case |
| binompdf | Exact probability | P(X = x) | One specific outcome |
| binomcdf | Cumulative | P(X ≤ x) | Multiple outcomes ≤ x |
1 – Binomcdf: At Least or More Than

Negative Binomial CDF (When to Use)
The negative binomial CDF is used when you’re counting the number of failures before a fixed number of successes.
Example:
What’s the probability that it takes at most 10 attempts to get 3 successful free throws?
This scenario cannot be solved using standard binomcdf. Use a Negative Binomial Calculator online for this purpose.
Common Mistakes by U.S. Students
- Confusing binompdf with binomcdf
- Not adjusting x – 1 when calculating “at least”
- Entering calculator values in the wrong order
- Assuming binomcdf gives two-tailed probabilities (it doesn’t)
FAQs
Q1. Can I use this method for the SAT?
Yes. It’s applicable to advanced probability questions. Calculators are allowed for most SAT math sections.
Q2. Is binomcdf available on TI-84 Plus CE?
Yes. Press 2nd → VARS to access the DISTR menu and select binomcdf.
Q3. Can I use binomcdf for “at least” problems?
Yes, use the complement:
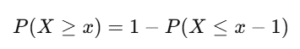
Q4. Is binomcdf always increasing?
Yes. CDF values increase as x increases, since they accumulate more probability mass.
Conclusion
The Binomial CDF Calculator is a critical tool for solving cumulative probability problems in U.S. statistics courses. Whether you’re using a TI-84, TI-83, or an online tool, understanding how and when to use binomcdf can help improve your performance on homework, tests, and standardized exams like the SAT, ACT, or AP Stats.
Disclaimer
This guide is for educational use. Please double-check your results when using for assignments or assessments, and consult your teacher if you’re unsure.