Welcome To Our Binomial PMF Calculator
Calculate exact probabilities using this Binomial PMF Calculator. Get step-by-step PMF values using the binomial formula with examples.
Binomial PMF Calculator
Table of Contents
Related Calculator:

How to Use the Binomial PMF Calculator
The Binomial PMF Calculator helps you calculate the exact probability of getting exactly k successes in n trials, where the probability of success in each trial is p. Follow these steps:
Step-by-Step Instructions
1. Enter the Number of Trials (n)
- This is the total number of independent experiments or trials.
- Example: If you flip a coin 10 times, n = 10.
2. Enter the Number of Successes (k)
- This is the number of desired successful outcomes.
- Example: You want to find the probability of getting exactly 4 heads, so k = 4.
3. Enter the Probability of Success (p)
- This is the chance of success in a single trial (a decimal between 0 and 1).
- Example: For a fair coin, p = 0.5; for a 30% chance, p = 0.3.
4. Click on the “Compute PMF” Button
- The calculator will display:
- The final PMF value (i.e., the probability that X = k)
- Step-by-step solution using the binomial formula
5. Read the Result and Explanation
You’ll see a formatted mathematical breakdown:
- The formula with your input values
- Factorials and powers calculated
- Final result rounded to 8 decimal places
Example
Let’s say you want to calculate:
What is the probability of getting exactly 5 successes in 12 trials, if each success has a probability of 0.3?
You would:
- Enter n = 12
- Enter k = 5
- Enter p = 0.3
- Click Compute PMF
The calculator will display:
- P(X = 5) ≈158P(X = 5)
- Full step-by-step math with factorials and exponents
Binomial PMF Calculator – Step-by-Step Probability Solver
Understanding how to calculate the Binomial Probability Mass Function (PMF) is essential for students in statistics, data science, and applied mathematics. Whether you’re preparing for exams, analyzing real-world data, or running simulations, this calculator simplifies your task by giving you the exact probability of k successes in n trials.
Use the interactive calculator below, and learn how the binomial PMF works, including its formula, step-by-step breakdown, and examples using real input values.
What is the Binomial PMF?
The Binomial PMF (Probability Mass Function) tells you the probability of getting exactly k successes in n independent trials, when each trial has a constant success probability p.
For example, if you’re flipping a coin 10 times (n = 10) and want the probability of getting exactly 4 heads (k = 4), the binomial PMF formula helps you compute this quickly.

Example: When n = 12, k = 5, and p = 0.3
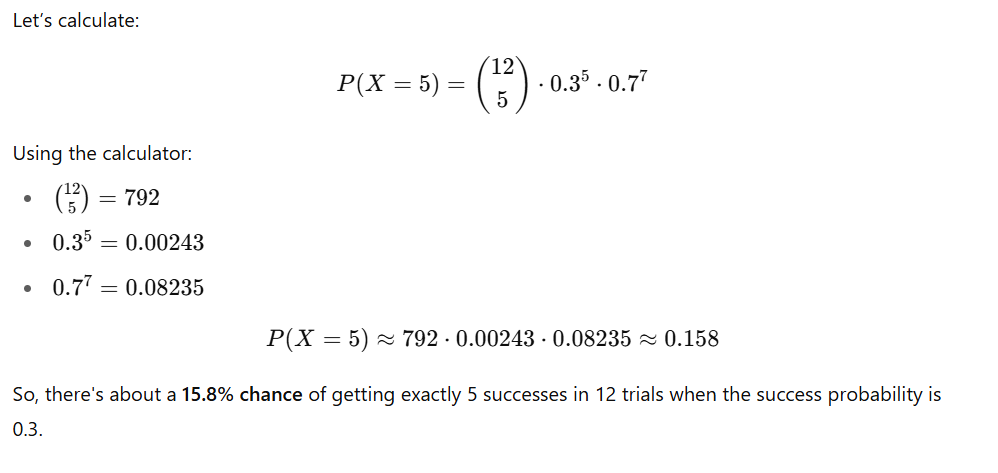
Step-by-Step Explanation by the Calculator
After entering your values, the calculator provides:
- The final PMF result (rounded to 8 decimal places)
- A step-by-step solution with factorials, powers, and intermediate values
- MathJax-rendered formulas to help you understand the math clearly
This is especially helpful for students and instructors in:
- AP Statistics (USA)
- GCSE/A-Level Maths (UK)
- Data Science & Machine Learning
- Probability Theory Courses
Applications of Binomial PMF
- Probability of passing or failing exams
- Quality control (defect rates in production)
- Survey results and market research
- Genetics and biology (inheritance modeling)
- A/B testing and web analytics
Troubleshooting & Input Validation
The calculator ensures:
- n, k, and p must be valid numbers
- 0 ≤ k ≤ n, and 0 ≤ p ≤ 1
- Automatic error messages if the input is invalid
Why Use This Calculator?
- Free and fast
- Mobile and desktop friendly
- Ideal for classroom learning and exam prep
- Step-by-step output helps you learn, not just compute
FAQs – Binomial PMF
Q1: What if k > n?
This is invalid, as you can’t have more successes than trials.
Q2: Can p be greater than 1 or less than 0?
No, probability must always be between 0 and 1.
Q3: What does the calculator use for factorials?
A JavaScript loop-based implementation is used to avoid performance issues with large numbers.
Q4: Is this calculator accurate?
Yes, it’s accurate up to 8 decimal places and uses the true mathematical formula.
Conclusion
The Binomial PMF Calculator is your one-click solution to finding exact probabilities in binomial distributions. With an intuitive interface and detailed breakdown of steps, it’s a perfect tool for students, teachers, researchers, and statisticians.
Try it now and make probability problems a breeze.
Disclaimer
This tool is for educational purposes only. Always verify results with certified statistical tools if used for professional or critical applications.