Learn what a binomial squared is, how to expand or factor it in 5 easy steps with formulas, examples, and a table. Perfect for exam preparation.
Why Binomial Squared is Important in Algebra
If you’re a student studying algebra or preparing for entrance exams like SAT, ACT, or any Indian competitive exams such as JEE or SSC, you’ve likely encountered expressions like (x + 3)^2. These are called binomial squares, and they play a fundamental role in algebraic simplification, solving quadratic equations, and graphing parabolas.

Understanding how to expand, simplify, and factor binomial squares can significantly improve your problem-solving skills. In this detailed guide, we will explain what a binomial squared is, provide the standard formulas, teach you how to identify patterns, and offer worked examples with step-by-step solutions.
This post is tailored for students who want clarity, exam-focused techniques, and a solid foundation in algebra.
What Is a Binomial Squared?
A binomial squared refers to the product of a binomial multiplied by itself. A binomial is an algebraic expression made up of two terms connected by a plus or minus sign, such as (x + y) or (a – b).
When you square a binomial, you’re multiplying it by itself:
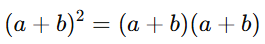
By applying the distributive property (also known as the FOIL method), this multiplication results in a trinomial: a^2 + 2ab + b^2
This expansion technique is critical for solving quadratic equations, simplifying expressions, and working with functions in vertex form.
Binomial Squared Formula
The most commonly used formulas for squaring a binomial are:

These formulas represent perfect square trinomials, and recognizing them helps you factor or expand expressions quickly.
Step-by-Step: How to Expand a Squared Binomial
Let’s walk through how to expand a binomial square using an example.
Example 1: Expand \( (x + 5)^2 \)
Step 1: Identify the binomial
Here, \( a = x \) and \( b = 5 \)
Step 2: Apply the formula
Step 3: Simplify the terms
So, \( (x + 5)^2 \) expands to \( x^2 + 10x + 25 \)
Example 2: Expand \( (3x – 2)^2 \)
This step-by-step expansion is useful when solving word problems or simplifying polynomial expressions in exams.
How to Factor a Binomial Squared
Sometimes you’re given a trinomial and asked to write it as a binomial squared. To do this, look for patterns in the expression that match the formulas mentioned earlier.
Example: Factor \( x^2 + 6x + 9 \)
Step 1: Identify first and last terms
\( x^2 = (x)^2 \) and \( 9 = (3)^2 \)
Step 2: Check the middle term
Is \( 6x = 2ab \)? Yes, because \( 2 \cdot x \cdot 3 = 6x \)
Factored form: \( (x + 3)^2 \)
Additional Example: Factor \( 4x^2 – 12x + 9 \)
So, the factored form is \( (2x – 3)^2 \)
How to Write a Trinomial as a Binomial Squared
To convert a trinomial to a binomial squared, ensure it matches this general form:
Example: Factor \( 25x^2 + 30x + 9 \)
Factored form: \( (5x + 3)^2 \)
Application in Quadratic Equations and Vertex Form
Binomial squares are essential when rewriting quadratic equations in vertex form. This process is known as completing the square.
Example: Rewrite \( x^2 + 8x + 10 \) in vertex form
Step 1:
Half of 8 = 4
Step 2:
Square it: \( 4^2 = 16 \)
Step 3:
Vertex form: \( (x + 4)^2 – 6 \)
Binomial Squared Table for Quick Reference
| Binomial | Expanded Form | Factored Form |
|---|---|---|
| \( (x + 4)^2 \) | \( x^2 + 8x + 16 \) | – |
| \( (x – 7)^2 \) | \( x^2 – 14x + 49 \) | – |
| – | \( x^2 + 10x + 25 \) | \( (x + 5)^2 \) |
| – | \( x^2 – 6x + 9 \) | \( (x – 3)^2 \) |
| – | \( 4x^2 – 20x + 25 \) | \( (2x – 5)^2 \) |
Derivative of a Binomial Squared (Advanced Concept)
Let’s say: \( f(x) = (x + 3)^2 \)
Apply the chain rule:
Binomial Squared Calculator and Tools
If you want to save time during practice, you can use a binomial squared calculator to expand or factor expressions instantly. Tools like these can help students verify answers quickly.
Try it here: Binomial Distribution Calculator – This site includes useful calculators and formula tools for binomial expressions and probability.
You can also download a PDF summary of binomial squared formulas and examples for revision purposes.
Frequently Asked Questions (FAQs)
Q1. What is a binomial squared in algebra?
A binomial squared is the result of multiplying a two-term expression by itself, like (a + b)^2, and it simplifies to a trinomial.
Q2. How can I quickly recognize a trinomial as a binomial squared?
Look for perfect square first and last terms and see if the middle term is twice their product.
Q3. Can I use a calculator to solve binomial squared problems?
Yes, online binomial squared calculators can help you verify results and save time in competitive exams.
Conclusion: Key Takeaways for Students
The concept of binomial squared is not only important for algebraic simplification but also forms the foundation for more advanced topics like quadratic equations, functions, and calculus. By understanding the expansion formula, recognizing perfect square trinomials, and using tools like calculators or the FOIL method, students can solve problems faster and more accurately.
Whether you’re preparing for your board exams, competitive tests, or university-level math, mastering binomial squares is a critical skill that will help you succeed.
Continue learning and practicing using online tools like Binomial Distribution Calculator for better accuracy and speed.
Disclaimer
This article is for educational purposes only. Students are advised to follow their syllabus and consult their instructors for exam-specific requirements.